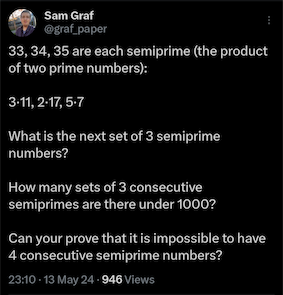
Here’s my solution to a lovely task that I saw posted on twitter the other day:

import math  
from itertools import combinations  

def isPrime(n):  
  if n == 1:  
    return False  
  elif n ==2:  
    return True  
  else:  
    for i in range (2,int(math.sqrt(n))+1):  
      if n%i==0:  
        return False  
  return True  

PrimeList = []  

for num in range (1,500):  
  if isPrime(num):  
    PrimeList.append(num)  

semiPrimeList = []  
    
for prime1, prime2 in combinations(PrimeList, 2):  
    product = prime1 * prime2  
    if product not in semiPrimeList:  
        semiPrimeList.append(product)  

semiPrimeList = sorted(semiPrimeList)  

consecutive_groups = []  
        
for i in range(len(semiPrimeList) - 2):  
  if semiPrimeList[i] + 1 == semiPrimeList[i + 1] and semiPrimeList[i + 1] + 1 == semiPrimeList[i + 2]:  
    consecutive_groups.append((semiPrimeList[i], semiPrimeList[i + 1], semiPrimeList[i + 2]))  

print(consecutive_groups)  

It gives an output like this:

[(33, 34, 35), (85, 86, 87), (93, 94, 95), (141, 142, 143), (201, 202, 203), (213, 214, 215), (217, 218, 219), (301, 302, 303), (393, 394, 395), (445, 446, 447), (633, 634, 635), (697, 698, 699), (921, 922, 923)]